9064. Старик и шахматная доска

За время своего путешествия Кратос побывал в множестве разных мест. Так, сегодня он забрел в маленькую деревушку, где его приютил седой старик, накормил и дал место для ночлега. Взамен старик попросил всего одну вещь – сделать для него шахматную доску, ведь он так любит эту игру.

У старика есть n белых и m черных квадратиков 1 * 1, из которых он хочет сделать не обычную доску 8 * 8, а наибольшую возможную, которая во-первых будет квадратной, а во-вторых будет иметь шахматную раскраску, то есть где любые две соседние по стороне клетки будут разных цветов (при этом угловые клетки могут быть как белого, так и черного цвета, в отличие от обычной шахматной доски). Кратос не совсем понял, зачем старику такая доска, но спорить не стал, и принялся за работу. Однако, с математикой у нашего титана совсем плохо, поэтому найти длину стороны квадрата, которая в итоге должна получиться, для него оказалось непосильной задачей, и он обратился за помощью к вам. Помогите ему – найдите максимальную длину шахматной доски, которую можно составить из имеющихся квадратиков.

Вход. Два целых числа n и m (0 ≤ n, m ≤ 10⁹) – количество белых и черных квадратиков соответственно. Гарантируется, что n + m > 0.

Выход. Выведите длину стороны максимального возможного квадрата, имеющего шахматную раскраску, который можно составить из имеющихся у старика квадратиков. Квадратики, конечно же, необязательно использовать все.

Пример входа 1	Пример выхода 1
8 9	4
Пример входа 2	Пример выхода 2
15 12	5

РЕШЕНИЕ

перебор - математика

Анализ алгоритма

Квадрат, содержащий n + m клеток, имеет длину стороны не более . Пусть x – длина стороны квадрата.

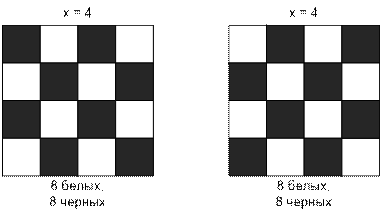
Если x четное, то в таком квадрате количество черных и белых клеток одинаково и равно x² / 2. Если x² / 2 ≤ n и x² / 2 ≤ m, то квадрат со стороной x можно составить из имеющихся у старика квадратиков.

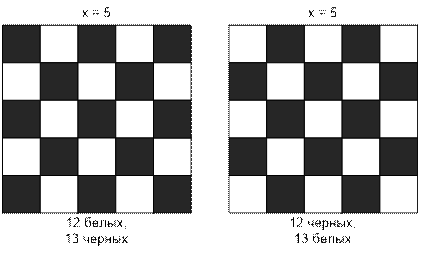
Если x нечетное, то в таком квадрате количество черных и белых клеток отличается на 1 и в зависимости от цвета покраски одного из углов может равняться:

· (x² – 1) / 2 белых и (x² + 1) / 2 черных;

· (x² – 1) / 2 черных и (x² + 1) / 2 белых;

Если количество белых и черных квадратов не более n и m, то квадрат со стороной x составить можно.

Перебираем значение x от до 1 и выводим первое такое число x, для которого существует искомый квадрат.

Реализация алгоритма

Читаем входные данные.

scanf("%d %d", &n, &m);

x = sqrt(n + m);

Перебираем возможную длину стороны квадрата.

for (i = x; i > 0; i--)

{

if (i % 2 == 0)

{

Длина стороны квадрата i четная. Если в наличии имеются i² / 2 белых и черных квадратов, то ответ найден.

q = i * i / 2;

if (n >= q && m >= q) break;

}

else

{

Длина стороны квадрата i нечетная. Если в наличии имеются (x² – 1) / 2 белых и (x² + 1) / 2 черных квадратиков или (x² – 1) / 2 черных и (x² + 1) / 2 белых квадратиков, то ответ найден.

q = (i * i - 1) / 2;

if (n >= q && m >= q + 1) break;

if (n >= q + 1 && m >= q) break;

}

}

Выводим ответ.

printf("%d\n", i);

Реализация алгоритма – формула

Читаем входные данные. Меняем местами n и m так чтобы было n ≤ m.

scanf("%d %d", &n, &m);

if (n > m) swap(n, m); // n <= m

Пусть длина x стороны квадрата четная. Поскольку x² / 2 ≤ n, то . Вычислим и проверим, является ли x четным. Если x нечетно, то уменьшим его на 1. Шахматную доску со стороной x можно составить.

x = int(sqrt(2 * n));

if (x % 2 == 1) x--;

res = x;

Пусть длина x стороны квадрата нечетная. Количество черных и белых квадратов должно отличаться на 1. Если n = m, то уменьшим n на 1.

if (n == m) n--;

Имеет место неравенство: (x² – 1) / 2 ≤ n, то есть . Вычислим и проверим, является ли x нечетным. Если x четное, то уменьшим его на 1. Шахматную доску со стороной x можно составить.

x = int(sqrt(2 * n + 1));

if (x % 2 == 0) x--;

if (x > res) res = x;

Выводим ответ.

printf("%d\n", res);